刷爆leetcode：贪心思想

简介

1 贪心思想(greedy algorithm)

1.1 贪心算法的基本思路

• （1） 建立数学模型来描述问题。

• （2） 把求解的问题分成若干个子问题。

• （3） 对每一子问题求解，得到子问题的局部最优解。

• （4） 把子问题的解局部最优解合成原来解问题的一个解。

1.2 贪心算法适用的问题

贪心策略的前提是：局部最优策略能导致产生全局最优解。

实际上，贪心算法使用的情况比较少，一般对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析可以做出判断。

实战演练

1 常见贪心

455. 分发饼干

leetcode

难度: 简单

这题比较简单，也非常经典，可以作为学习贪心思想的开胃菜。

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

贪心题解

• 局部最优->全局最优
• 局部最优：小尺寸饼干给胃口小的小孩
• 全局最优：优先满足胃口小的小孩

当然也可以偶先考虑满足胃口大的小孩。

不能把小尺寸的给大胃口的吃，因为吃不饱。
也不能把大尺寸的给小尺寸的吃，因为浪费。

优先满足胃口小的小孩code，注释部分为优先考虑胃口大的。

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort() #g.sort(reverse=True)
        s.sort() #s.sort(reverse=True)
        g_i = 0
        s_i = 0
        sum = 0
        while g_i < len(g) and s_i < len(s):
            if g[g_i] <= s[s_i]:
                sum += 1
                g_i += 1
                s_i += 1
            else:
                s_i += 1 #g_i += 1
        return sum

435. 无重叠区间

leetcode

难度: 中等

难度升级的经典题，需要一定的思考。
如何移除最少的区间呢？
逆向思考一下：如何保留最多的区间呢？（移除数=总数-保留数）
是不是简单多了？

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

贪心题解

具体思路如图所示：

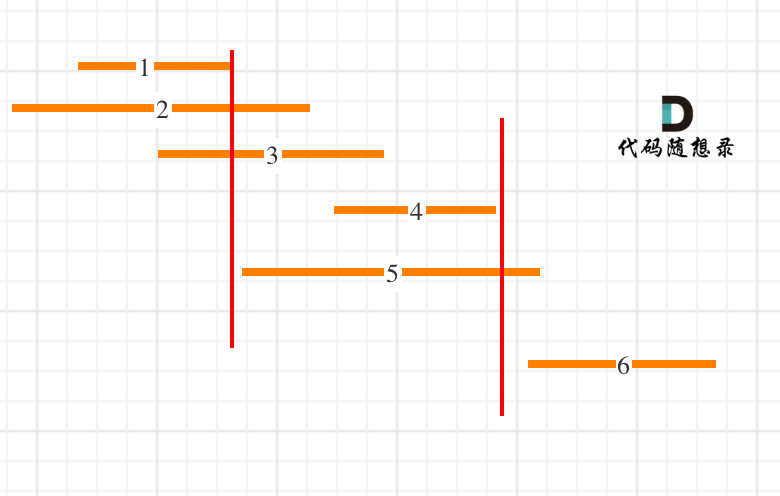
其实，这题就是会议预定类型的题，如果我们把本题的区间看成是会议，那么按照右端点排序，我们一定能够找到一个最先结束的会议。而这个会议一定是我们需要添加到最终结果的的首个会议。
所以我们要使用左区间排序（当然其实右区间也是可以的，不过就是从右往左遍历而已（md，为何多此一举））

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        sum = 0
        right = -60000
        intervals.sort(key = lambda c: (c[1]), reverse=False)
        for L in intervals:
            if L[0] >= right:
                 sum += 1
                 right = L[1]
        return len(intervals) - sum

452. 用最少数量的箭引爆气球

leetcode

难度: 中等

这题的解法其实和上一题435不能说一模一样，只能说完全一致。

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

贪心题解

具体思路略。

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        points.sort(key= lambda c: (c[1]),reverse=False)
        right = -2**31 - 1
        sum = 0
        for p in points:
            if p[0] > right:
                right = p[1]
                sum += 1
        return sum

406. 根据身高重建队列

leetcode

难度: 中等

这题还是有一定思考难度的，看了题解才知道咋做的（其实我也忘了自己有没有看题解……）
反正是个脑筋急转弯。

套路：一般这种数对，还涉及排序的，根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队

贪心题解

具体思路如下：

假设有打乱顺序 意味着原始的数组满足排序

• 第一个数字，第一优先级排序，由高到低，是为了用下标就能表示前面有几个元素比当前元素 大于等于
• 第二个数字，第二优先级排序，由低到高，当身高一样的时候，人数少的就应该放前面（正确性保障）
  先安排身高最高且前面人最少的站好。
  然后从左到右依次插入，插入位置为其第2项，即有多少人在他前面。
  [[7, 0], [7, 1], [6, 1], [5, 0], [5, 2], [4, 4]]

[7, 0]
[7, 0], [7, 1]
[7, 0], [6, 1], [7, 1],
[5, 0], [7, 0], [7, 1], [6, 1]
[5, 0], [7, 0], [5, 2], [7, 1], [6, 1]
[5, 0], [7, 0], [5, 2], [6, 1], [4, 4], [7, 1]

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
        people.sort(key = lambda c : (-c[0],c[1]), reverse = False)
        res = []
        for p in people :
            res.insert(p[1],p)
        return res

121. 买卖股票的最佳时机

leetcode

难度: 简单

炒股？那必然贪心！别人恐惧我贪婪，别人贪婪我恐惧！
动态规划其实也算是贪心吧？！

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

贪心题解

具体思路如下：
总的老说，就是找到最低价和最高价（当然最低价要在最高价前面）。
所以我们要遍历所有节点，记录当前节点时我们可以得到的最大收益。
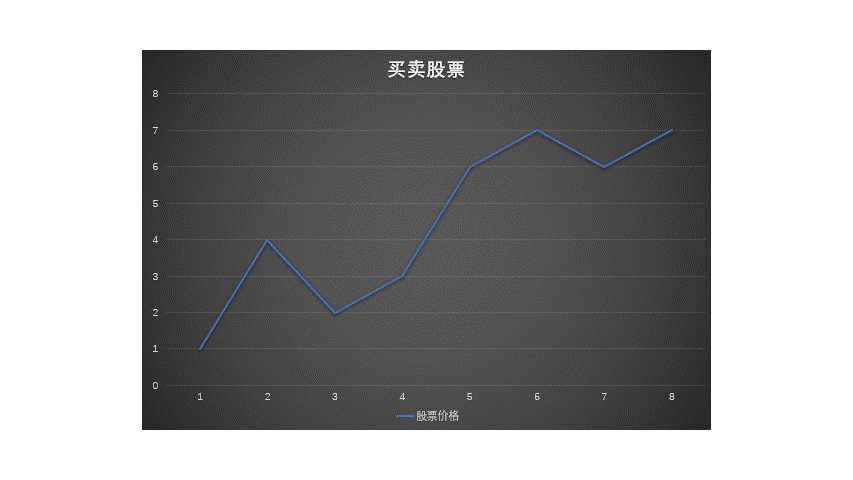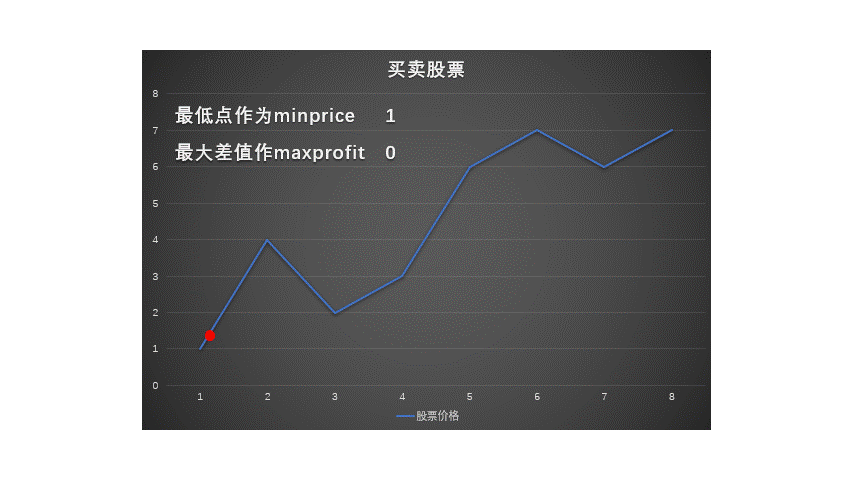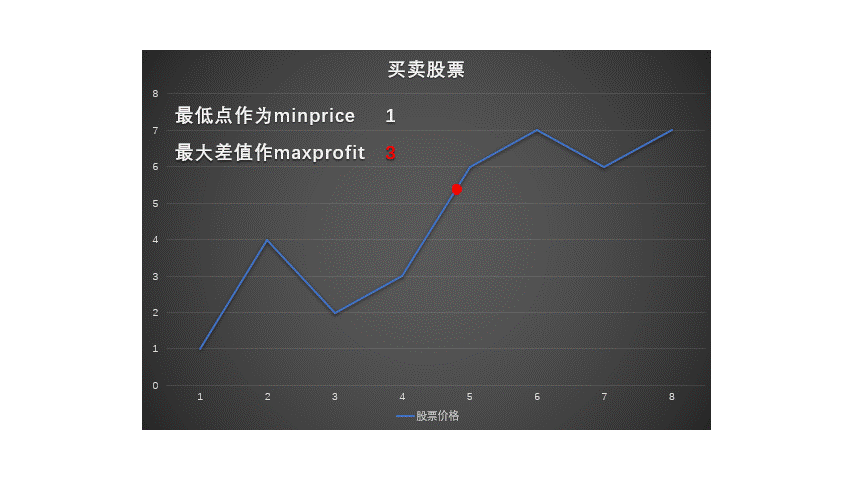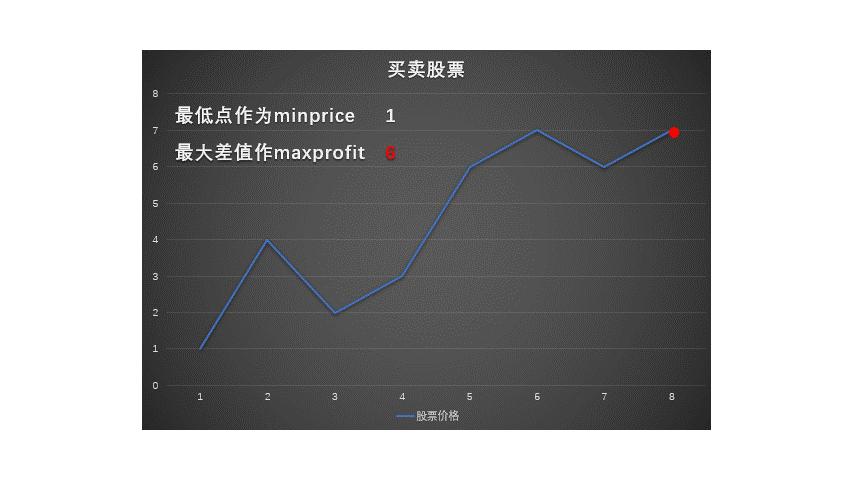
如何计算呢？

• 当前最大收益 = max(已知最大收益, 当前价 - 前面已被记录的最低价)
  over.

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        res = 0
        mip = prices[0]
        for i in range(1,len(prices)):
            p = prices[i]
            if p < mip :
                mip = p
            else:
                res = max(res,p-mip)
        return res

122. 买卖股票的最佳时机 II

leetcode

难度: 中等

上一题的升级版！别人恐惧我贪婪，别人贪婪我恐惧！

note：你在任何时候 最多 只能持有 一股 股票。你也可以购买它，然后在 同一天 出售。

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
  随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

贪心题解

具体思路如下：
尽量的频繁交易，第一天买第二天就卖，不能拖！当然这是要建立在第二天价格高于第一天的前提下。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        res = 0
        tmp = prices[0]
        for p in prices:
            if p > tmp:
                res += p - tmp
            tmp = p
        return res

605. 种花问题

leetcode

难度: 简单

跳格子！

输入：flowerbed = [1,0,0,0,1], n = 1
输出：true

贪心题解

具体思路如下：
能种就种。

class Solution:
    def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:
        res = 0
        l = len(flowerbed)
        i = 0
        while i < len(flowerbed):
            if flowerbed[i] == 1:
                i += 1
                continue
            if l == 1 and flowerbed[0] == 0:
                res += 1
            elif i == 0 and flowerbed[i+1] != 1:
                res += 1
                i += 1
            elif i == l - 1 and flowerbed[i-1] != 1:
                res += 1
                i += 1
            elif flowerbed[i-1] != 1 and flowerbed[i+1] != 1:
                res += 1
                i += 1
            i += 1
        if n <= res:
            return True
        else:
            return False

665. 非递减数列

leetcode

难度: 中等

我发现贪心思想都有点脑筋急转弯~

输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个 4 变成 1 来使得它成为一个非递减数列。

贪心题解

具体思路如下：
本题是要维持一个非递减的数列，所以遇到递减的情况时（nums[i] > nums[i + 1]），要么将前面的元素缩小，要么将后面的元素放大。

但是本题唯一的易错点就在这:

• 如果将nums[i]缩小，可能会导致其无法融入前面已经遍历过的非递减子数列；
• 如果将nums[i + 1]放大，可能会导致其后续的继续出现递减；
  所以要采取贪心的策略，在遍历时，每次需要看连续的三个元素，也就是瞻前顾后，遵循以下两个原则：
• 需要尽可能不放大nums[i + 1]，这样会让后续非递减更困难；
• 如果缩小nums[i]，但不破坏前面的子序列的非递减性；

算法步骤：

• 遍历数组，如果遇到递减：
  • 还能修改：
    • 修改方案1：将nums[i]缩小至nums[i + 1]；
    • 修改方案2：将nums[i + 1]放大至nums[i]；
  • 不能修改了：直接返回false；

class Solution:
    def checkPossibility(self, nums: List[int]) -> bool:
        length = len(nums)
        cnt = 0
        for i in range(length - 1):
            if nums[i] > nums[i + 1]:
                cnt += 1
                if cnt == 2:
                    return False
                if i != 0 and nums[i - 1] > nums[i + 1]:
                    nums[i + 1] = nums[i] 
                else:
                    nums[i] = nums[i + 1]
        return True

53. 最大子数组和

leetcode

难度: 简单

此简单非彼简单，动态规划就行了。

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

贪心题解

具体思路如下：
重点在nums[i] += max(nums[i-1], 0)
要么nums[i] = nums[i] + nums[i-1] 前一项大于0，能让他变大
要么nums[i] = nums[i] 前一项不大于0，不能让他变大

遍历序号	nums	res
0	[-2, 1, -3, 4, -1, 2, 1, -5, 4]	-2
1	[-2, 1, -3, 4, -1, 2, 1, -5, 4]	1
2	[-2, 1, -2, 4, -1, 2, 1, -5, 4]	1
3	[-2, 1, -2, 4, -1, 2, 1, -5, 4]	4
4	[-2, 1, -2, 4, 3, 2, 1, -5, 4]	4
5	[-2, 1, -2, 4, 3, 5, 1, -5, 4]	5
6	[-2, 1, -2, 4, 3, 5, 6, -5, 4]	6
7	[-2, 1, -2, 4, 3, 5, 6, 1, 4]	6
8	[-2, 1, -2, 4, 3, 5, 6, 1, 5]	6

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res = nums[0]
        for i in range(1,len(nums)):
            nums[i] += max(nums[i-1], 0)
            if nums[i] > res:
                res = nums[i]
        return res

763. 划分字母区间

leetcode

难度: 中等

有一说一，贪心思想真的绕弯弯！！！

输入：S = “ababcbacadefegdehijhklij”
输出：[9,7,8]
解释：
划分结果为 “ababcbaca”, “defegde”, “hijhklij”。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 的划分是错误的，因为划分的片段数较少。

贪心题解

具体思路如下：
首先呢，用字典记录所有出现字母的出现位置start和消失位置end
然后呢，把所有的[start, end]组成一个新数组[[start0, end0], [start1, end1], …, [startN, endN]]，不用特意去排序，因为上一步找出来的[start, end]本来就是按start从小到大排序的
再后呢，开始遍历了，如果当前节点的start_i落在了前一个节点的[start_i-1, end_i-1]里面，就说明两个点重叠了，一旦发现这个条件不成立，就将end - start + 1加入结果，然后更新start和end。

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        hmpend = {}
        hmpstart = {}
        for i in range(len(s)):
            if s[i] not in hmpstart:
                hmpstart[s[i]] = i
            hmpend[s[i]] = i
        dlist = []
        for k in hmpstart:
            dlist.append([hmpstart[k],hmpend[k]])
        # dlist.sort(key=lambda c:(c[0],c[1])) # 其实并不需要排序
        start = 0
        end = 0
        res = []
        for dl in dlist:
            if start <= dl[0] and dl[0] <= end:
                end = max(end, dl[1])
            else:
                res.append(end - start + 1)
                start = dl[0]
                end = dl[1]
        res.append(end - start + 1)
        return res